As mentioned before, we’ll generally use the letter a to denote the side opposite angle A, the letter b to denote the side opposite angle B, and the letter c to denote the side opposite angle C. Since the sum of the angles in a triangle equals 180°, and angle C is 90°, that means angles A and B add up to 90°, that is, they are complementary angles. Therefore the cosine of B equals the sine of A. We saw on the last page that sin A was the opposite side over the hypotenuse, that is, a/c. Hence, cos B equals a/c. In other words, the cosine of an angle in a right triangle equals the adjacent side divided by the hypotenuse:

The Pythagorean identity for sines and cosines
Recall the Pythagorean theorem for right triangles. It says that
where c is the hypotenuse. This translates very easily into a Pythagorean identity for sines and cosines. Divide both sides by c2 and you get
But a2/c2 = (sin A)2, and b2/c2 = (cos A)2. In order to reduce the number of parentheses that have to be written, it is a convention that the notation sin2 A is an abbreviation for (sin A)2, and similarly for powers of the other trig functions. Thus, we have proven that
when A is an acute angle. We haven’t yet seen what sines and cosines of other angles should be, but when we do, we’ll have for any angle θ one of most important trigonometric identities, the Pythagorean identity for sines and cosines:
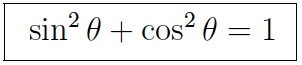
Sines and cosines for special common angles
We can easily compute the sines and cosines for certain common angles. Consider first the 45° angle. It is found in an isosceles right triangle, that is, a 45°-45°-90° triangle. In any right triangle c2 = a2 + b2, but in this one a = b, so c2 = 2a2. Hence c = a√2. Therefore, both the sine and cosine of 45° equal 1/√2 which may also be written √2 / 2.Next consider 30° and 60° angles. In a 30°-60°-90° right triangle, the ratios of the sides are 1 : √3 : 2. It follows that sin 30° = cos 60° = 1/2, and sin 60° = cos 30° = √3 / 2.
These findings are recorded in this table.
| Angle | Degrees | Radians | cosine | sine |
|---|---|---|---|---|
 | 90° | π/2 | 0 | 1 |
 | 60° | π/3 | 1/2 | √3 / 2 |
 | 45° | π/4 | √2 / 2 | √2 / 2 |
 | 30° | π/6 | √3 / 2 | 1/2 |
| 0° | 0 | 1 | 0 |
Exercises
These exercises all refer to right triangles with the standard labelling.30. b = 2.25 meters and cos A = 0.15. Find a and c.
33. b = 12 feet and cos B = 1/3. Find c and a.
35. b = 6.4, c = 7.8. Find A and a.
36. A = 23° 15', c = 12.15. Find a and b.
Hints
30. The cosine of A relates b to the hypotenuse c, so you can first compute c. Once you know b and c, you can find a by the Pythagorean theorem.
33. You know b and cos B. Unfortunately, cos B is the ratio of the two sides you don’t know, namely, a/c. Still, this gives you an equation to work with: 1/3 = a/c. Then c = 3a. The Pythagorean theorem then implies that a2 + 144 = 9a2. You can solve this last equation for a and then find c.
35. b and c give A by cosines and a by the Pythagorean theorem.
36. A and c give a by sines and b by cosines.
Answers
30. c = b/cos A = 2.25/0.15 = 15 meters; a = 14.83 meters.
33. 8a2 = 144, so a2 = 18. Therefore a is 4.24', or 4'3".
c = 3a which is 12.73', or 12'9".
35. cos A = b/c = 6.4/7.8 = 0.82. Therefore A = 34.86° = 34°52', or about 35°.
a2 = 7.82 – 6.42 = 19.9, so a is about 4.5.
36. a = c sin A = 12.15 sin 23°15' = 4.796.
b = c cos A = 12.15 cos 23°15' = 11.17.