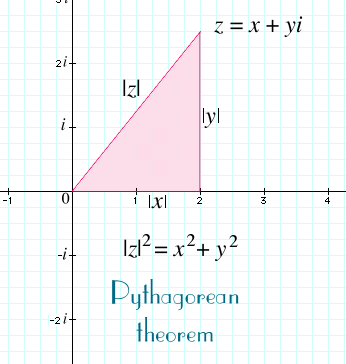
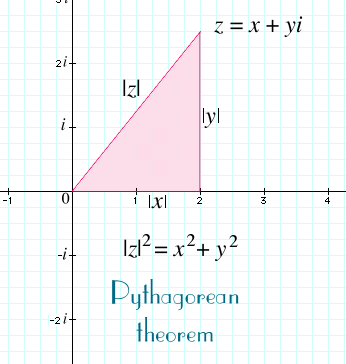
For a complex number z = x + yi, we define the absolute value |z| as being the distance from z to 0 in the complex plane C. This will extend the definition of absolute value for real numbers, since the absolute value |x| of a real number x can be interpreted as the distance from x to 0 on the real number line. We can find the distance |z| by using the Pythagorean theorem. Consider the right triangle with one vertex at 0, another at z and the third at x on the real axis directly below z (or above z if z happens to be below the real axis). The horizontal side of the triangle has length |x|, the vertical side has length |y|, and the diagonal side has length |z|. Therefore,
(Note that for real numbers like x, we can drop absolute value when squaring, since |x|2 = x2.) That gives us a formula for |z|, namely,

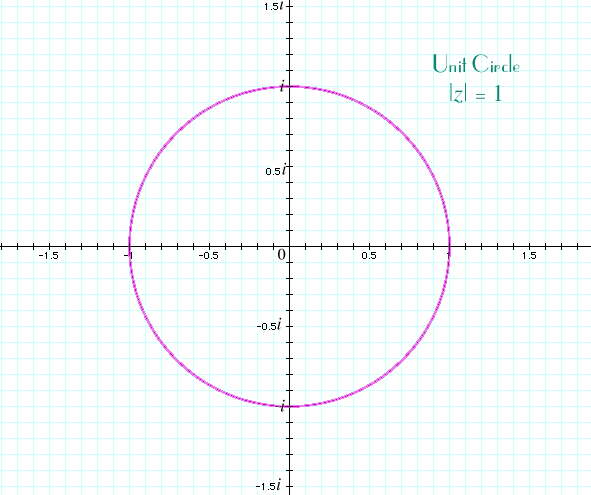
A complex number z = x + yi will lie on the unit circle when x2 + y2 = 1. Some examples, besides 1, –1, i, and –1 are ±√2/2 ± i√2/2, where the pluses and minuses can be taken in any order. They are the four points at the intersections of the diagonal lines y = x and y = x with the unit circle. We'll see them later as square roots of i and –i.
You can find other complex numbers on the unit circle from Pythagorean triples. A Pythagorean triple consists of three whole numbers a, b, and c such that a2 + b2 = c2 If you divide this equation by c2, then you find that (a/c)2 + (b/c)2 = 1. That means that a/c + i b/c is a complex number that lies on the unit circle. The best known Pythagorean triple is 3:4:5. That triple gives us the complex number 3/5 + i 4/5 on the unit circle. Some other Pythagorean triples are 5:12:13, 15:8:17, 7:24:25, 21:20:29, 9:40:41, 35:12:27, and 11:60:61. As you might expect, there are infinitely many of them. (For a little more on Pythagorean triples, see the end of the page at http://www.clarku.edu/~djoyce/trig/right.html.)
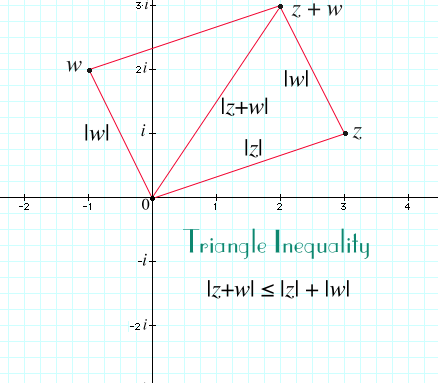
There's an important property of complex numbers relating addition to absolute value called the triangle inequality. If z and w are any two complex numbers, then

You can see this from the parallelogram rule for addition. Consider the triangle whose vertices are 0, z, and z + w. One side of the triangle, the one from 0 to z + w has length |z + w|. A second side of the triangle, the one from 0 to z, has length |z|. And the third side of the triangle, the one from z to z + w, is parallel and equal to the line from 0 to w, and therefore has length |w|. Now, in any triangle, any one side is less than or equal to the sum of the other two sides, and, therefore, we have the triangle inequality displayed above.