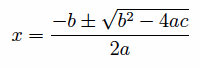
where a, b, and c are constants. We also know that the general solution is given by the quadratic formula:
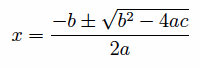
where there are two distinct real solutions if the discriminant b2 – 4ac is positive, one double real solution if the discriminant is 0, and no real solutions if the discriminant is negative.
Back in the 15th century, this was not understood. Instead, quadratic equations were classified into four different kinds depending on the signs of the coefficients a, b, and c. Since the leading coefficient a is not zero in a quadratic equation, you can always divide by it to get an equivalent quadratic equation where a equals 1, that is, x2 + bx + c = 0. This one form gives rise to four forms when you move the negative terms to the other side of the equation and when you drop zero terms from the equation:
| x2 | = | c |
| x2 + bx | = | c |
| x2 + c | = | bx |
| x2 | = | bx + c |
There are other forms, but either they have no solutions among the positive numbers or else they can be reduced to linear equations. Each of these forms required a different form of a solution. With hindsight, we see that the 15th century solutions are just special cases of the quadratic formula. One would think that the consolidation of four cases into one might be enough justification for accepting negative numbers, but apparently it wasn't. It seems to take a lot of time before people will extend their concept of number to include new entities.

As with the quadratic equation, there are several forms for the cubic when negative terms are moved to the other side of the equation and zero terms dropped.
Back in the 16th century it was a big deal to solve cubic equations. There was a great controversy in Italy between Cardano (1501–1576) and Tartaglia (1499–1557) about who should get credit for solving the cubic equation. Any book on the history of mathematics will go into the details of this fascinating controversy. What’s interesting to us, though, is that negative numbers were becoming legitimatized, a deeper insight into equations was developed, and the first inkling of a complex number appeared. Incidentally, at this time symbolic algebra had not been developed, so all the equations were written in words instead of symbols!
Cardano, in his Artiss Magnæ, or Great Art, found negative solutions to equations, and he called these numbers “fictitious”. He also noted an important fact connecting solutions of a cubic equation to its coefficients, namely, the sum of the solutions is the negation of b, the coefficient of the x2 term. At one other point, he mentions that the problem of dividing 10 into two parts so that their product is 40 would have to be 5 + √(–15) and 5 – √(–15).
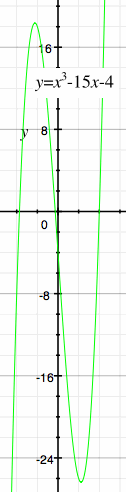
Cardano did not go further into what later became to be called complex numbers than that observation, but a few years later Bombelli (1526–1572) gave several examples involving these new beasts. Here’s one example.
One of Cardano’s cubic formulas gives the solution to the equation x3 = cx + d as
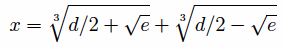
where e = (d/2)2 – (c/3)3). Bombelli used this to solve the equation x3 = 15x + 4 to get the solution
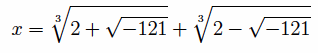
Now, the square root of –121 is not a real number; it’s neither positive, negative, nor zero. Bombelli continued to work with this expression until he found equations that lead him to the solution 4. He determined that
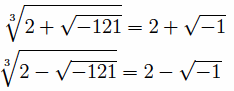
and, therefore, the solution x = 4. You can check those equations are correct by cubing 2 ± √–1 to get 2 ± 11√–1.
This example is not given to show that Bombelli knew everything there is to know about complex numbers, only that he was starting to understand them.