Since Gauss proved the Fundamental Theorem of Algebra, we know that all complex numbers are of the form x + yi, where x and y are real numbers, real numbers being all those numbers which are positive, negative, or zero. Therefore, we can use the xy-plane to display complex numbers. We'll even call it the complex plane when we use the xy-plane that way. That gives us a second way to complex numbers, the first way being algebraically as in the expression x + yi.

Notation.
The standard symbol for the set of all complex numbers is C, and we'll also refer to the complex plane as C.
We'll try to use x and y for real variables, and z and w for complex variables. For example, the equation z = x + yi is to be understood as saying that the complex number z is the sum of the real number x and the real number y times i. In general, the x part of a complex number z = x + yi is called the real part of z, while y is called the imaginary part of z. (Sometimes yi is called the imaginary part.)
When we use the xy-plane for the complex plane C, we'll call the x-axis by the name real axis, and the y-axis we'll call the imaginary axis.
Real numbers are to be considered as special cases of complex numbers; they're just the numbers
x + yi when y is 0, that is, they're the numbers on the real axis. For instance, the real number 2 is 2 + 0i. The numbers on the imaginary axis are sometimes called purely imaginary numbers.
Arithmetic operations on C
The operations of addition and subtraction are easily understood. To add or subtract two complex numbers, just add or subtract the corresponding real and imaginary parts. For instance, the sum of 5 + 3i and 4 + 2i is 9 + 5i. For another, the sum of 3 + i and –1 + 2i is 2 + 3i.
Addition can be represented graphically on the complex plane C. Take the last example. The complex number z = 3 + i is located 3 units to the right of the imaginary axis and 1 unit above the real axis, while w = –1 + 2i is located 1 unit left and 2 units up. So the sum z + w = 2 + 3i is 2 units right and 3 units up.

Parallelogram Rule.
Note in the last example that the four complex numbers 0, z = 3 + i, w = –1 + 2i, and z + w = 2 + 3i are the corners of a parallelogram. This is generally true. To find where in the plane C the sum z + w of two complex numbers z and w is located, plot z and w, draw lines from 0 to each of them, and complete the parallelogram. The fourth vertex will be z + w.
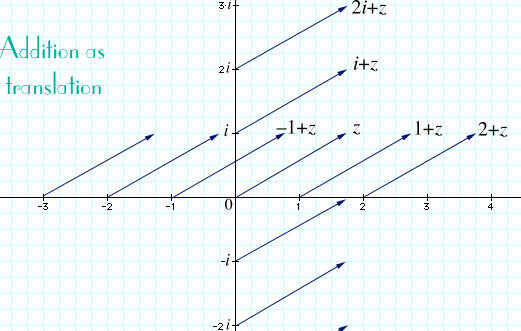
Addition as translation.
Using the parallelogram rule can interpret addition by w as a transformation of the plane C. Adding w to 0 gives w, of course, so 0 is moved to w in this transformation. Any other point z is moved to z + w, so z is moved in the same direction the same distance. In other words, every point in
C is moved the same direction and distance when w is added to it. We can say that addition by w gives a translation the plane C in the direction and distance from 0 to w. The term "vector" is usually used in the description: "the plane is translated along the vector 0w.
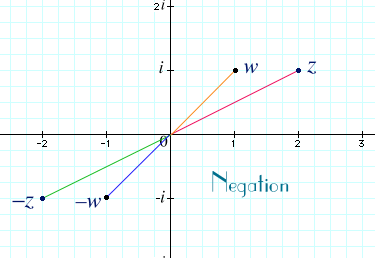
Negation and Subtraction.
There's a nice geometric interpretation of negation, too. Of course, the negation of x + yi is –x – yi, so the negation of a complex number will be located just opposite 0 and the same distance away. For example, z = 2 + i is located 2 units right and one unit up, so its negation –z = –2 – i is located 2 units left and one unit down.
Negation can be interpreted as a transformation of the plane C, too. If you rotate the plane 180° around 0, then every point z is sent to its negation –z. Thus, negation gives a 180° rotation.
From addition and negation, you can determine what the geometric rule is for subtraction. To find where z – w will be, first negate w by finding the point opposite 0, then use the parallelogram rule.
We can interpret subtraction of w as a transformation of C: the plane is translated along the vector from 0 to –w.
Another way of saying that is that the plane is translated along the vector w0.




