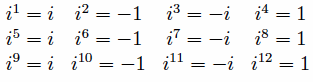
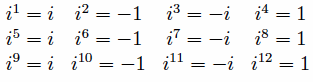
and so forth. The reasons were that (1) the absolute value |i| of i was one, so all its powers also have absolute value 1 and, therefore, lie on the unit circle, and (2) the argument arg(i) of i was 90°, so its nth power will have argument n90°, and those angles will repeat in a period of length 4 since 4·90° = 360°, a full circle.
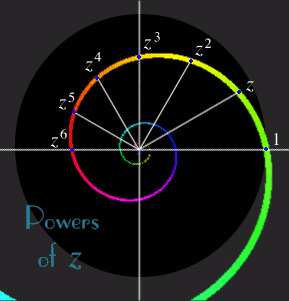
More generally, you can find zn as the complex number (1) whose absolute value is |z|n, the nth power of the absolute value of z, and (2) whose argument is n times the argument of z.
In the figure you see a complex number z whose absolute value is about the sixth root of 1/2, that is, |z| = 0.89, and whose argument is 30°. Here, the unit circle is shaded black while outside the unit circle is gray, so z is in the black region. Since |z| is less than one, it’s square is at 60° and closer to 0. Each higher power is 30° further along and even closer to 0. The first six powers are displayed, as you can see, as points on a spiral. This spiral is called a geometric or exponential sprial.
There are, in fact, six sixth roots of any complex number. Let w be a complex number, and z any of its sixth roots. Since z6 = w, it follows that
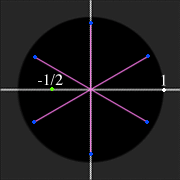 For example, take w to be -1/2, the green dot in the figure to the right. Then |w| is 1/2, and arg(w) is 180°. Let z be a sixth root of w. Then (1) |z| is |w|1/6 which is about 0.89. Also, (2) the argument of w is arg(w) = 180°. But the same angle could be named by any of
For example, take w to be -1/2, the green dot in the figure to the right. Then |w| is 1/2, and arg(w) is 180°. Let z be a sixth root of w. Then (1) |z| is |w|1/6 which is about 0.89. Also, (2) the argument of w is arg(w) = 180°. But the same angle could be named by any of
If we take 1/6 of each of these angles, then we’ll have the possible arguments for z:
Since each of the angles for z differs by 360°, therefore each of the possible angles for z will differ by 60°. These six sixth roots of -1/2 are displayed in the figure as blue dots.
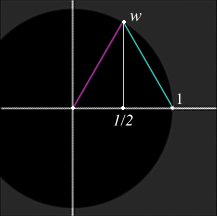 Let’s consider now the sixth roots of unity. They will be placed around the circle at 60° intervals. Two of them, of course, are ±1. Let w be the one with argument 60°. The triangle with vertices at 0, 1, and w is an equilateral triangle, so it is easy to determine the coordinates of w. The x-coordinate is 1/2, and the y-coordinate is √3/2. Therefore, w is (1 + i√3)/2. The remaining sixth roots are reflections of w in the real and imaginary axes. In summary, the six sixth roots of unity are ±1, and (±1 ± i√3)/2 (where + and – can be taken in any order).
Let’s consider now the sixth roots of unity. They will be placed around the circle at 60° intervals. Two of them, of course, are ±1. Let w be the one with argument 60°. The triangle with vertices at 0, 1, and w is an equilateral triangle, so it is easy to determine the coordinates of w. The x-coordinate is 1/2, and the y-coordinate is √3/2. Therefore, w is (1 + i√3)/2. The remaining sixth roots are reflections of w in the real and imaginary axes. In summary, the six sixth roots of unity are ±1, and (±1 ± i√3)/2 (where + and – can be taken in any order).
Now some of these sixth roots are lower roots of unity as well. The number –1 is a square root of unity, (–1 ± i√3)/2 are cube roots of unity, and 1 itself counts as a cube root, a square root, and a “first” root (anything is a first root of itself). But the remaining two sixth roots, namely, (1 ± i√3)/2, are sixth roots, but not any lower roots of unity. Such roots are called primitive, so (1 ± i√3)/2 are the two primitive sixth roots of unity.
It’s fun to find roots of unity, but we’ve found most of the easy ones already.