Proposition 12
Let AB be the given infinite straight line, and C the given point which is not on it.
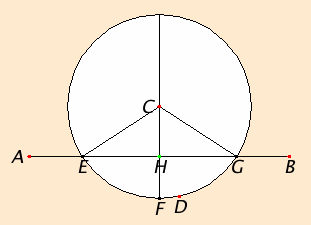
It is required to draw a straight line perpendicular to the given infinite straight line AB from the given point C which is not on it.
Take an arbitrary point D on the other side of the straight line AB, and describe the circle EFG with center C and radius CD. Bisect the straight line EG at H, and join the straight lines CG, CH, and CE.
I say that CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.
Since GH equals HE, and HC is common, therefore the two sides GH and HC equal the two sides EH and HC respectively, and the base CG equals the base CE. Therefore the angle CHG equals the angle EHC, and they are adjacent angles.
But, when a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
Therefore CH has been drawn perpendicular to the given infinite straight line AB from the given point C which is not on it.