Proposition 19
Let ABC be a triangle having the angle ABC greater than the angle BCA.
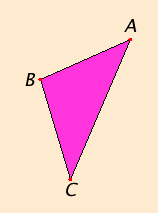
I say that the side AC is greater than the side AB.
If not, either AC equals AB or it is less than it.
Now AC does not equal AB, for then the angle ABC would equal the angle ACB, but it does not. Therefore AC does not equal AB.
Neither is AC less than AB, for then the angle ABC would be less than the angle ACB, but it is not. Therefore AC is not less than AB.
And it was proved that it is not equal either. Therefore AC is greater than AB.
Therefore in any triangle the side opposite the greater angle is greater.