Proposition 34
Let ACDB be a parallelogrammic area, and BC its diameter.
I say that the opposite sides and angles of the parallelogram ACDB equal one another, and the diameter BC bisects it.
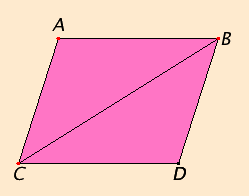
Since AB is parallel to CD, and the straight line BC falls upon them, therefore the alternate angles ABC and BCD equal one another.
Again, since AC is parallel to BD, and BC falls upon them, therefore the alternate angles ACB and CBD equal one another.
Therefore ABC and DCB are two triangles having the two angles ABC and BCA equal to the two angles DCB and CBD respectively, and one side equal to one side, namely that adjoining the equal angles and common to both of them, BC. Therefore they also have the remaining sides equal to the remaining sides respectively, and the remaining angle to the remaining angle. Therefore the side AB equals CD, and AC equals BD, and further the angle BAC equals the angle CDB.
Since the angle ABC equals the angle BCD, and the angle CBD equals the angle ACB, therefore the whole angle ABD equals the whole angle ACD.
And the angle BAC was also proved equal to the angle CDB.
Therefore in parallelogrammic areas the opposite sides and angles equal one another.
I say, next, that the diameter also bisects the areas.
Since AB equals CD, and BC is common, the two sides AB and BC equal the two sides DC and CB respectively, and the angle ABC equals the angle BCD. Therefore the base AC also equals DB, and the triangle ABC equals the triangle DCB.
Therefore the diameter BC bisects the parallelogram ACDB.
Therefore in parallelogrammic areas the opposite sides and angles equal one another, and the diameter bisects the areas.