Proposition 5
Let ABC be an isosceles triangle having the side AB equal to the side AC, and let the straight lines BD and CE be produced further in a straight line with AB and AC.
I say that the angle ABC equals the angle ACB, and the angle CBD equals the angle BCE.
Take an arbitrary point F on BD. Cut off AG from AE the greater equal to AF the less, and join the straight lines FC and GB.
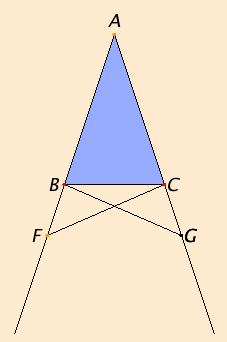
Since AF equals AG, and AB equals AC, therefore the two sides FA and AC equal the two sides GA and AB, respectively, and they contain a common angle, the angle FAG.
Therefore the base FC equals the base GB, the triangle AFC equals the triangle AGB, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides, that is, the angle ACF equals the angle ABG, and the angle AFC equals the angle AGB.
Since the whole AF equals the whole AG, and in these AB equals AC, therefore the remainder BF equals the remainder CG.
But FC was also proved equal to GB, therefore the two sides BF and FC equal the two sides CG and GB respectively, and the angle BFC equals the angle CGB, while the base BC is common to them. Therefore the triangle BFC also equals the triangle CGB, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides. Therefore the angle FBC equals the angle GCB, and the angle BCF equals the angle CBG.
Accordingly, since the whole angle ABG was proved equal to the angle ACF, and in these the angle CBG equals the angle BCF, the remaining angle ABC equals the remaining angle ACB, and they are at the base of the triangle ABC. But the angle FBC was also proved equal to the angle GCB, and they are under the base.
Therefore in isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another.