Proposition 14
Let AB and CD be equal straight lines in a circle ABDC.
I say that AB and CD are equally distant from the center.
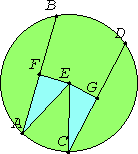
Take the center E of the circle ABDC. Draw EF and EG from E perpendicular to AB and CD, and join AE and EC.
Then, since a straight line EF passing through the center cuts a straight line AB not passing through the center at right angles, it also bisects it. Therefore AF equals FB. Therefore AB is double AF.
For the same reason CD is also double CG. But AB equals CD, therefore AF also equals CG.
Also, since AE equals EC, the square on AE also equals the square on EC. But the sum of the squares on AF and EF equals the square on AE, for the angle at F is right, and the sum of the squares on EG and GC equals the square on EC, for the angle at G is right. Therefore the sum of the squares on AF and FE equals the sum of the squares on CG and GE, of which the square on AF equals the square on CG, for AF equals CG. Therefore the remaining square on FE equals the square on EG. Therefore EF equals EG.
But straight lines in a circle are said to be equally distant from the center when the perpendiculars drawn to them from the center are equal. Therefore AB and CD are equally distant from the center.
Next, let the straight lines AB and CD be equally distant from the center, that is, let EF equal EG.
I say that AB also equals CD.
For, with the same construction, we can prove, as before, that AB is double AF, and CD double CG. And, since AE equals CE, the square on AE equals the square on CE. But the sum of the squares on EF and FA equals the square on AE, and the sum of the squares on EG and GC equals the square on CE.
Therefore the sum of the squares on EF and FA equals the sum of the squares on EG and GC, of which the square on EF equals the square on EG, for EF equals EG. Therefore the remaining square on AF equals the square on CG. Therefore AF equals CG. And AB is double AF, and CD double CG, therefore AB equals CD.
Therefore equal straight lines in a circle are equally distant from the center, and those which are equally distant from the center equal one another.