
Rather than repeating what he did for chords, let’s look at how to create tables for sines and cosines using his methods. First, based on the Pythagorean theorem and similar triangles, the sines and cosines of certain angles can be computed directly. In particular, you can directly find the sines and cosines for the angles 30°, 45°, and 60° as described in the section on cosines. Ptolemy knew two other angles that could be constructed, namely 36° and 72°. These angles were constructed by Euclid in Proposition IV.10 of his Elements. Like Ptolemy, we can use that construction to compute the trig functions for those angles. At this point we could compute the trig functions for the angles 30°, 36°, 45°, 60°, and 72°, and, of course we know the values for 0° and 90°, too.
Keep in mind that if you know the sine of an angle θ, then you know the cosine of the complementary angle 90° – θ; likewise, if you know then cosine of an angle θ then you know the sine of the complementary angle 90° – θ:

So you have the trig functions for 18° and 54°, too.
Next, you can use the half-angle formulas for sines and cosines to compute the values for half of an angle if you know the values for the angle. If θ is an angle between 0° and 180°, then
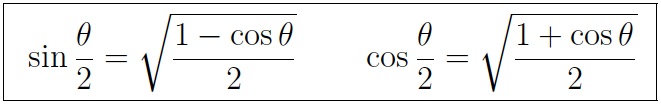
Using these, from the values for 18°, 30°, and 54°, you can find the values for 27°, 15°, and 9°, and, therefore, their complements 63°, 75°, and 81°.
With the help of the sum and difference formulas
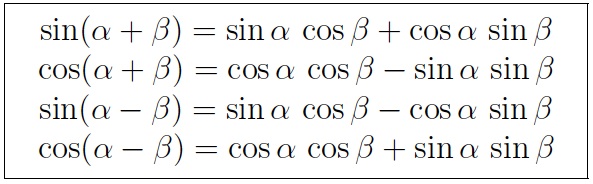
you can find the sine and cosine for 3° (from 30° and 27°) and then fill in the tables for sine and cosine for angles from 0° though 90° in increments of 3°.
Again, using half-angle formulas, you could produce a table with increments of 1.5° (that is, 1° 30'), then 0.75° (which is 45'), or even of 0.375° (which is 22' 30"). But how do you get a table with 1° increments? Ptolemy recognized that there was no Euclidean construction to trisect an angle of 3° to get an angle of 1°, but since the sine function is almost linear for small angles, you could approximate sin 1° just by interpolating a third of the way beteen the values of sin 0.75° and sin 1.5°. With that step, we can construct trig tables for trig functions with increments of 1°.
Better trig tables have been created throughout the centuries. For instance, Ulugh Beg (15th century) constructed sine and tangent tables for every minute of arc to about nine digits of accuracy!
| Ulugh Beg (1394–1449) | |||
|---|---|---|---|
|
|||
 Ulugh Beg Observatory, Samarkand, Uzbekistan
Ulugh Beg Observatory, Samarkand, Uzbekistan
|
|||
Incidentally, if you have a table of sines, you can read it in reverse to compute arcsine, so only one table is needed for both.
In the late 17th century, Newton and other mathematicians developed power series. A power series is like a polynomial of unbounded degree. For the various trig functions, these mathematicians found power series. Here are the power series for sine and cosine (where x is an angle measured in radians):
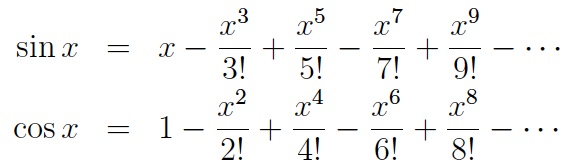
The three dots ... mean that the expression is to go on forever, adding another term, then subtracting a term, etc. The exclamation point ! is to be read “factorial”, and it means you multiply together the whole numbers from 1 up through the given number. For example, 5!, “five factorial”, equals 1 times 2 times 3 times 4 times 5, which is 120, and so, 6! = 720.
These power series have infinitely many terms, but they get small so very fast that only the first few terms contribute much.
Suppose you want to compute the sine of 45°, correct to some number of places, using this power series. First convert 45° to radians to get π/4, which is 0.78539816 to eight places. Then compute the value of
A little bit of analysis is needed to determine how many terms of the power series are needed to achieve the desired accuracy. Also, certain other tricks can be used to speed up the computations. In any case, the essential idea is to use the first few terms of a power series to compute trig functions.
The power series for the rest of the trig functions and the power series for the inverse trig functions can be found in most books on calculus that discuss power series.