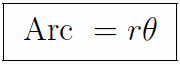
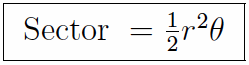
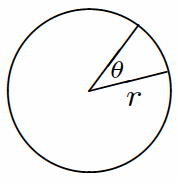
You can easily find both the length of an arc and the area of a sector for an angle θ in a circle of radius r.
| Length of an arc. The length of the arc is just the radius r times the angle θ where the angle is measured in radians. To convert from degrees to radians, multiply the number of degrees by π/180. | 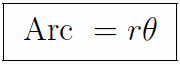
|
| Area of a sector. The area of the sector is half the square of the radius times the angle, where, again, the angle is measured in radians. | 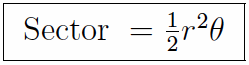
|
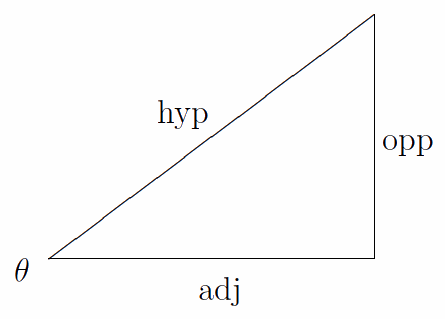
The most important formulas for trigonometry are those for a right triangle. If θ is one of the acute angles in a triangle, then the sine of theta is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side.



|
These three formulas are collectively known by the mnemonic SohCahToa. Besides these, there’s the all-important Pythagorean formula that says that the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Along with the knowledge that the two acute angles are complementary, that is to say, they add to 90°, you can solve any right triangle:
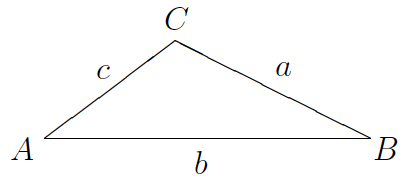
These formulas work for any triangle whether acute, obtuse, or right. We’ll use the standard notation where the three vertices of the triangle are denoted with the uppercase letters A, B, and C, while the three sides opposite them are respectively denoted with lowercase letters a, b, and c.
There are two important formulas for oblique triangles. They’re called the law of cosines and the law of sines.
The law of cosines generalizes the Pythagorean formula to all triangles. It says that c2, the square of one side of the triangle, is equal to a2 + b2, the sum of the squares of the the other two sides, minus 2ab cos C, twice their product times the cosine of the opposite angle. When the angle C is right, it becomes the Pythagorean formula.
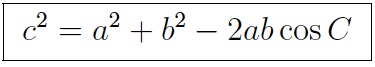
The law of sines says that the ratio of the sine of one angle to the opposite side is the same ratio for all three angles.
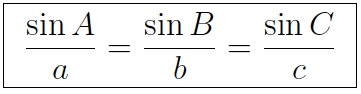
With these two formulas you can solve any triangle:
There are three different useful formulas for the area of a triangle, and which one you use depends on what information you have.
| Half the base times the height. This is the usual one to use since it’s simplest and you usually have that information. Choose any side to call the base b. Then if h is the distance from the opposite vertex to b, then the area is half of bh. | 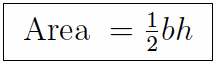
|
| Heron’s formula. This is useful when you know the three sides a, b, and c of the triangle, and all you want to know is the area. Let s be half their sum, called the semiperimeter. Then the area is the square root of the product of s, s − a, s − b, and s − c. | 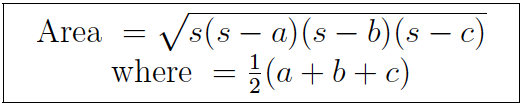
|
| Side-angle-side formula. Use this when you know two sides, a and b, and the included angle, C. The area is half the product of the two sides times the sine of the included angle. | 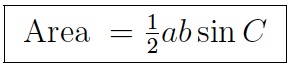
|