Trigonometric Functions

Arbitrary angles and the unit circle

The ancient Greek geometers only considered angles between 0° and 180°, and they considered neither the straight angle of 180° nor the degenerate angle of 0° to be angles. It’s not only useful to consider those special cases to be angles, but also to include angles between 180° and 360°, too, sometimes called “reflex angles.” With the applications of trigonometry to the subjects of calculus and differential equations, angles beyond 360° and negative angles became accepted, too.

Consider the unit circle. Denote its center (0,0) as O, and denote the point (1,0) on it as A. As a moving point B travels around the unit circle starting at A and moving in a counterclockwise direction, the angle AOB as a 0° angle and increases. When B has made it all the way around the circle and back to A, then angle AOB is a 360° angle. Of course, this is the same angle as a 0° angle, so we can identify these two angles. As B continues the second time around the circle, we get angles ranging from 360° to 720°. They’re the same angles we saw the first time around, but we have different names for them. For instance, a right angle is named as either 90° or 450°. Each time around the circle, we get another name for the angle. So 90°, 450°, 810° and 1170° all name the same angle.

If B starts at the same point A and travels in the clockwise direction, then we’ll get negative angles, or more precisely, names in negative degrees for the same angles. For instance, if you go a quarter of a circle in the clockwise direction, the angle AOB is named as –90°. Of course, it’s the same as a 270° angle.

So, in summary, any angle is named by infinitely many names, but they all differ by multiples of 360° from each other.

Sines and cosines of arbitrary angles

Properties of sines and cosines that follow from this definition

1. Sine and cosine are periodic functions of period 360°, that is, of period 2π. That’s because sines and cosines are defined in terms of angles, and you can add multiples of 360°, or 2π, and it doesn’t change the angle. Thus, for any angle θ,
   sin (θ + 360°) = sin θ, and

   cos (θ + 360°) = cos θ.

   Many of the modern applications of trigonometry follow from the uses of trig to calculus, especially those applications which deal directly with trigonometric functions. So, we should use radian measure when thinking of trig in terms of trig functions. In radian measure that last pair of equations read as

   sin (θ + 2π) = sin θ, and

   cos (θ + 2π) = cos θ.

2. Sine and cosine are complementary:
   cos θ = sin (π/2 – θ)

   sin θ = cos (π/2 – θ)

   We’ve seen this before, but now we have it for any angle θ. It’s true because when you reflect the plane across the diagonal line y = x, an angle is exchanged for its complement.

3. The Pythagorean identity for sines and cosines follows directly from the definition. Since the point B lies on the unit circle, its coordinates x and y satisfy the equation x² + y² =1. But the coordinates are the cosine and sine, so we conclude
   sin² θ +  cos² θ = 1.

   We’re now ready to look at sine and cosine as functions.

4. Sine is an odd function, and cosine is an even function. You may not have come across these adjectives “odd” and “even” when applied to functions, but it’s important to know them. A function f  is said to be an odd function if for any number x, f(–x) = –f(x). A function f is said to be an even function if for any number x, f(–x) = f(x). Most functions are neither odd nor even functions, but some of the most important functions are one or the other. Any polynomial with only odd degree terms is an odd function, for example, f(x) = x⁵ + 8x³ – 2x. (Note that all the powers of x are odd numbers.) Similarly, any polynomial with only even degree terms is an even function. For example, f(x) = x⁴ – 3x² – 5. (The constant 5 is 5x⁰, and 0 is an even number.)

   Sine is an odd function, and cosine is even

   sin (–θ) = –sin θ, and

   cos (–θ) = cos θ.

   These facts follow from the symmetry of the unit circle across the x-axis. The angle –t is the same angle as t except it’s on the other side of the x-axis. Flipping a point (x,y) to the other side of the x-axis makes it into (x,–y), so the y-coordinate is negated, that is, the sine is negated, but the x-coordinate remains the same, that is, the cosine is unchanged.

5. An obvious property of sines and cosines is that their values lie between –1 and 1. Every point on the unit circle is 1 unit from the origin, so the coordinates of any point are within 1 of 0 as well.

The graphs of the sine and cosine functions

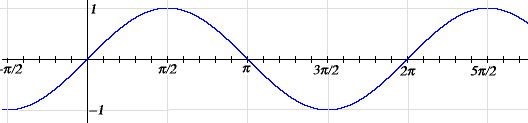
First, note that it is periodic of period 2π. Geometrically, that means that if you take the curve and slide it 2π either left or right, then the curve falls back on itself. Second, note that the graph is within one unit of the t-axis. Not much else is obvious, except where it increases and decreases. For instance, sin t grows from 0 to π/2 since the y-coordinate of the point B increases as the angle AOB increases from 0 to π/2.

Next, let’s look at the graph of cosine. Again, take the horizontal axis to be the t-axis, but now take the vertical axis to be the x-axis, and graph the equation x = cos t.

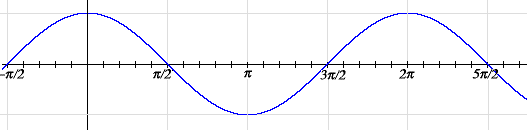
Note that it looks just like the graph of sin t except it’s translated to the left by π/2. That’s because of the identity cos t = sin (π/2 + t). Although we haven’t come across this identity before, it easily follows from ones that we have seen: cos t = cos –t = sin (π/2 – (–t)) = sin (π/2 + t).

The graphs of the tangent and cotangent functions

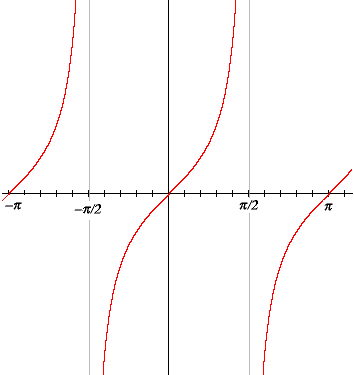
You can also see that tangent has period π; there are also vertical asymptotes every π units to the left and right. Algebraically, this periodicity is expressed by tan (t + π) = tan t.

The graph for cotangent is very similar.

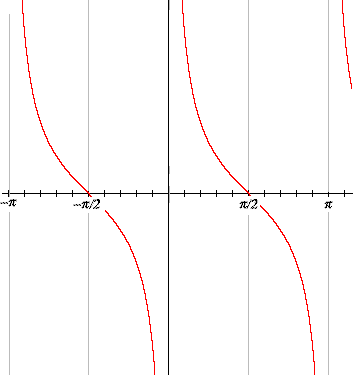
This similarity is simply because the cotangent of t is the tangent of the complementary angle π – t.

The graphs of the secant and cosecant functions

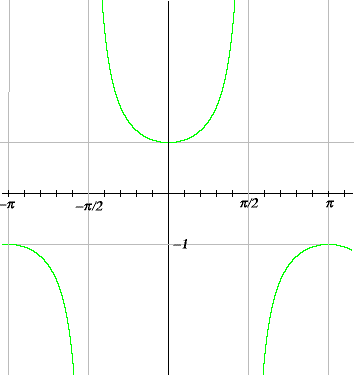
As you would expect by now, the graph of the cosecant looks much like the graph of the secant.