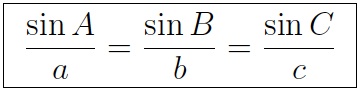
| This is an optional section. When learning how to use trigonometry to solve
oblique triangles, it is most important to know when and how to use these two laws.
If that’s enough for you, then just skip on to the next section on
area of a triangle. But if you’re interested in why
they’re true, then continue on.
As usual, we’ll use a standard notation for the angles and sides of a triangle. That means the side a is opposite the angle A, the side b is opposite the angle B, and the side c is opposite the angle C. |
|
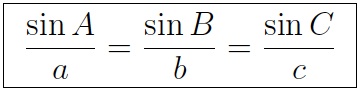
It’s enough to show the last equation
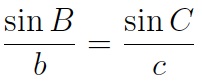
An explanation of the law of sines is fairly easy to follow, but in some cases we’ll have to consider sines of obtuse angles.
First, drop a perpendicular line AD from A down to the base BC of the triangle. The foot D of this perpendicular will lie on the edge BC of the triangle when both angles B and C are acute. But if angle B is obtuse, then the foot D will lie on BC extended in the direction of B. Yet if angle C is obtuse, then D will line on BC extended in the direction of C. Fortunately, the argument is the same in all three cases.
Let h denote the length of this line AD, that is, the height (or altitude) of the triangle.
When angle B is acute, then sin B = h/c. But this is true even when B is an obtuse angle as in the third diagram. There, angle ABC is obtuse. But the sine of an obtuse angle is the same as the sine of its supplement. That means sin ABC is the same as sin ABD, that is, they both equal h/c.
Likewise, it doesn’t matter whether angle C is acute or obtuse, sin C = h/b in any case.
These two equations tell us that h equals both c sin B and b sin C. But from the equation c sin B = b sin C, we can easily get the law of sines:
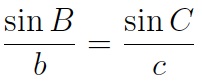
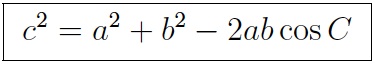
There are two other versions of the law of cosines,
Since the three verions differ only in the labelling of the triangle, it is enough to verify one just one of them. We’ll consider the version stated first.
In order to see why these laws are valid, we’ll have to look at three cases. For case 1, we’ll take the angle C to be obtuse. In case 2, angle C will be a right angle. In case 3, angle C will be acute.
| Case 1. For this case, we take angle C to be obtuse. This case has a wrinkle in it since the cosine of an obtuse angle is negative. Let’s see how that goes. | |||||||||||||
| First, drop a perpendicular line AD from A down to the base BC of
the triangle. In this case, the foot D of this perpendicular will lie outside the
triangle. Let h denote the height of the triangle, let d denote BD, and let e denote CD.
We can derive the following equations from the figure:
In general, the cosine of an obtuse angle is the negation of the cosine of its supplement. In this case that means the cosine of angle C, that is to say angle ACB, is the negation of the cosine of angle ACD. That’s why the minus sign appears in the last equation. |
| ||||||||||||
These equations and plain algebra finish the argument as follows:
| c2 | = | d2 + h2 |
| = | (a + e)2 + h2 | |
| = | a2 + 2ae + e2 + h2 | |
| = | a2 + b2 + 2ae | |
| = | a2 + b2 – 2ab cos C |
Thus, the law of cosines is valid when C is an obtuse angle.
Case 2. Now consider the case when the angle at C is right. The cosine of a right angle is 0, so the law of cosines, c2 = a2 + b2 – 2ab cos C, simplifies to becomes the Pythagorean identity, c2 = a2 + b2, for right triangles which we know is valid.
Case 3. In this case we assume that the angle C is an acute triangle. Drop a perpendicular line AD from A down to the base BC of the triangle. The foot D of the perpendicular will (1) lie on the edge BC if angle B is acute, (2) coincide with the point B if the angle B is right, or (3) lie on the side BC extended if the angle B is obtuse.
Let h denote the height of the triangle, let d denote BD, and e denote CD.
Then we can read the following relationships from the diagram:
| c2 | = | d2 + h2 |
| b2 | = | e2 + h2 |
| cos C | = | e/b |
| d2 | = | (e — a)2 |
That last equation requires explanation. If the point D lies on the side BC, then d = a – e, but if D lies on BC extended, then d = e – a. In either case, d2 = (e – a)2.
These equations and a little algebra finish the proof as follows:
| c2 | = | d2 + h2 |
| = | d2 – e2 + b2 | |
| = | (d – e) (d + e) + b2 | |
| = | (a – 2e) a + b2 | |
| = | a2 + b2 – 2ae | |
| = | a2 + b2 – 2ab cos C |
Thus, we now know that the law of cosines is valid when both angle C is acute, and we’ve finished all three cases.
Incidentally, Euclid included in his Elements a couple of propositions, II.12 and II.13, that look very much like the law of cosines, but they are not actually the law of cosines, of course, since trigonometry had not been developed in Euclid’s time.