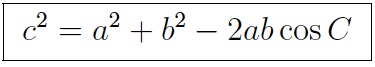
Let’s agree to a convention for labelling the parts of oblique triangles generalizing the convention for right triangles. Let the angles be labelled A, B, and C, and let the sides opposite them be labelled a, b, and c, respectively.
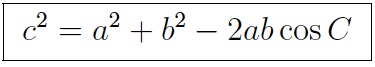
It looks like the Pythagorean theorem except for the last term, and if C happens to be a right angle, that last term disappears (since the cosine of 90° is 0), so the law of cosines is actually a generalization of the Pythagorean theorem.
Note that each triangle gives three equations for the law of cosines since you can permute the letters as you like. The other two versions are then a2 = b2 + c2 – 2bc cos A, and b2 = c2 + a2 – 2ca cos B.
The law of cosines relates the three sides of the triangle to one of the angles. You can use it in a couple of ways.
First, if you know one angle and the two adjacent sides, then you can determine the opposite side. For instance, if angle C = 60°, side a = 5, and side b = 8, then the law of cosines says c2 = 25 + 64 – 80 cos 60°. Since the cosine of 60° is 1/2, that equation simplifies to c2 = 49, so c = 7.
Second, if you know all three sides of a triangle, then you can use it to find any angle. For instance, if the three sides are a = 5, b = 6, and c = 7, then the law of cosines says 49 = 25 + 36 – 60 cos C, so cos C = 12/60 = 0.2, and, with the use of a calculator, C = 1.3734 radians = 78.69°.
Note: When triangle is obtuse, the cos C is negative. Suppose the three sides are a = 5, b = 6, and c = 10. Then the law of cosines says 100 = 25 + 36 – 60 cos C, so cos C = - 49/60 = - 0.81667. As you can see in the graphs on the previous page, the cosine of an obtuse angle is negative. This is fine, and your calculator will compute the arccosine properly. You’ll get C = 2.2556 radians = 129.237°.
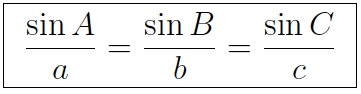
Note that the law of sines says that three ratios are equal. Like the law of cosines, you can use the law of sines in two ways.
First, if you know two angles and the side opposite one of them, then you can determine the side opposite the other one of them. For instance, if angle A = 30°, angle B = 45°, and side a = 16, then the law of sines says (sin 30°)/16 = (sin 45°)/b. Solving for b gives b = 16(sin 45°)/(sin 30°) = 22.6274.
Second, if you know two sides and the angle opposite one of them, then you can almost determine the angle opposite the other one of them. For instance, if side a = 25, side b = 15, and angle A = 40°, then the law of sines says (sin 40°)/25 = (sin B)/15. Solving for sin B gives sin B = 15 (sin 40°)/25 = 0.38567. Now, the arcsin of 0.38567 = 22.686°.
Warning: you may not have the correct answer. There are two angles between 0 and 180° with a given sine; the second one is the supplement of the first. So in this case, the second one is the obtuse angle 180 – 22.686 = 157.314°. This situation is indeterminant. Knowing two sides and the angle opposite one of them is not always enough to determine the triangle. There is no deterministic "side-side-angle" congruence theorem in geometry.
553. AB is a line 652 feet long on one bank of a stream, and C is a point on the opposite bank. A = 53° 18', and B = 48° 36'. Find the width of the stream from C to AB.
557. In a triangle ABC, a = 700 feet, B = 73° 48', and C = 37° 21'. If M is the middle point of BC find the length of AM, and the angles BAM and MAC.
561. Three circles of radii 3, 4, and 5 touch each other externally. Find the angles of the triangle formed by joining their centers.
563. A and B are points on opposite sides of a river. On one bank the line AC 650 feet is measured. The angle A = 73° 40', and C = 52° 38'. Find AB.
570. P and Q are two inaccessible points. To find the distance between them, a point A is taken in QP produced, and a line AB 1200 feet long is measured making the angle PAB = 26° 35'. The angle ABP = 48° 12' and ABQ = 106° 42'. How long is PQ?
579. The sides of a parallelogram are AB = 209.16 and AD =347.25, and the diagonal AC = 351.47. Find the angles and the other diagonal.
580. In a parallelogram ABCD, the diagonal AC = 521.16, than angle ABC = 110° 48' 12", and BAC = 27° 19' 36". Find the lengths of the sides and the other diagonal.
586. The diagonals of a parallelogram are 374.14 and 427.21 and the included angle is 70° 12' 38". Find the sides.
590. The sides of a quadrilateral in order are 763.83, 721.75, 547.12, and 593.21, and the angle between the first two sides is 53° 13' 12". Find the other three angles.
593. A and B are two points on opposite sides of a body of water, and soundings are to be taken in the line AB at points one quarter, one half, and three quarters of the distance from A to B. On the shore a line AC 1200 feet long is measured, and angles BAC = 63° 19' and ACB = 78° 43'. What angles must be turned off from CA at C in order to line up the boat from which the soundings are made at the proper points on AB?
608. On one side of a stream lines PA = 586.3 feet, PB = 751.6 feet are measures, angle APB being 167° 36'. Q is a point on the opposite side of the stream. Angle PAQ = 63° 18' and PBQ = 49° 24'. Find PQ.
612. To find the distance between two inaccessible points P and Q, a line AB 763.4 feet long is laid off so that AB produced intersects PQ externally [that is, the two line segments AB and PQ don’t intersect]. The angles PAB = 98° 47', QAB = 41° 36', PBA = 37° 16', and QBA = 94° 12'. Find the length of PQ.
553. You can use the law of sines to determine either of the lengths AB or BC. The question is to find the distance from C to AB. That means you drop a perpendicular from C to that line and determine its length. You could use the angle A and the line AC to find it, or you could use the angle B and the line BC to find it.
557. Same hint as 553.
561. The circles are tangent, so a line from one center to another is the sum of the radius of one circle and that of the other. You’ve got a triangle with sides 7, 8, and 9. You can use the law of cosines to find the angles.
563. The law of sines works well here.
570. Draw the figure. To find PQ, first find AP and AQ. You can find AP using the law of sines on triangle ABP, and you can find AQ using the law of sines on triangle ABQ.
579. You know the sides of triangles ABC and ADC, so you can determine their angles. In triangle ABD you then know an angle and the two adjacent sides, so you can find the opposite side BD.
580. First solve the triangle ABC. Next in triangle ABD you know two sides and you can easily determine the angle BAD.
586. The "included angle" is one of the two angles between the two diagonals. The other included angle is its supplement 180° – 70° 12' 38". Let P be the point where the two diagonals meet. It is the midpoint of each diagonal, so you know the distance between P and any vertex. Use the law of cosines to on two triangles with vertices P and two of the vertices of the parallelogram.
590. You know the sides of the quadrilateral ABCD and the angle at B. You can solve triangle ABC. Then you know all the sides of triangle ACD, so you can find its angles.
593. First determine the distance AB using the law of sines. Then for each of the proper positions of the boat P, you know two sides and the included angle of the triangle PAC, so you can determine the needed angle using the law of cosines.
608. First solve the triangle APB. Then you’ll have enough information to solve the triangle AQB.
612. There are several ways to solve this one. Here’s one way. Determine PA using the law of sines for triangle PAB, and determine QA using the law of sines for triangle QAB. Then use the law of cosines for triangle PAQ.
553. 345.43 feet.
557. 490.83 feet.
561. 48 ° 11' 24", 58 ° 24' 42", 73° 23' 54".
563. 640 feet 10 inches.
570. 651.9 feet.
579. 106° 18' 46", 73° 41' 14", 452.92.
580. 255.93, 372.11, 369.22.
586. 231.94, 328.93.
590. 125° 6' 12", 70° 57' 54", 110° 42' 42".
593. 23° 27', 47° 58, 66° 34'.
608. 854.6 feet.
612. 920.76 feet.