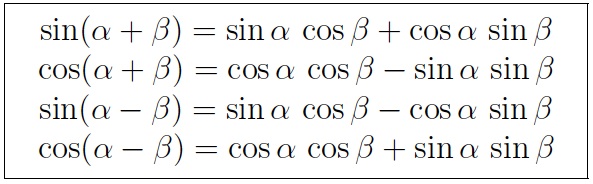
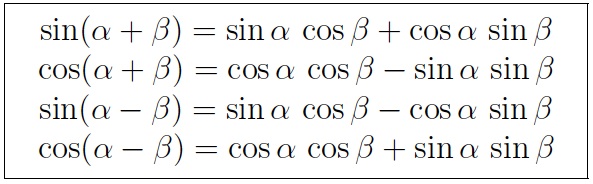
You can use these identities without knowing why they’re true. If you’re interested in why, then keep reading, otherwise, skip on to the next page.
In order to prove his sum and difference forumlas, Ptolemy first proved what we now call Ptolemy’s theorem.
We won't prove Ptolemy’s theorem here. The proof depends on properties of similar triangles and on the Pythagorean theorem. Instead, we’ll use Ptolemy’s theorem to derive the sum and difference formulas. |
|
We’ll follow Ptolemy’s proof, but modify it slightly to work with modern sines. Let O to be the center of a circle of radius 1, and take one of the lines, AC, to be a diameter of the circle. We’ll interpret each of the lines AC, BD, AB, CD, AD, and BC in terms of sines and cosines of angles. We already know AC = 2.
|
|
Let α be ∠BAC. Recall that the sine of an angle is half the chord of twice the angle. Euclid’s proposition III.20 says that the angle at the center of a circle twice the angle at the circumference, therefore ∠BOC equals 2α. Thus, the sine of α is half the chord of ∠BOC, so it equals BC/2, and so BC = 2 sin α. Let β be ∠CAD. That’s half of ∠COD, so sin β equals CD/2, and CD = 2 sin β. Then α + β is ∠BAD, so BD = 2 sin (α + β). We still have to interpret AB and AD. The line segment AB is twice the sine of ∠ACB. Triangle ABC is a right triangle by Thale’s theorem (Euclid’s proposition III.31: an angle in a semicircle is right). Therefore sin ∠ACB cos α. Hence, AB = 2 cos α. Likewise, AD = 2 cos β. Now we can write Ptolemy’s theorem in terms of sines and cosines. It says After dividing by 4, we get the addition formula for sines.
|
For example, take AD to be a diameter, α to be ∠BAD, and β to be ∠CAD, then you can directly show the difference formula for sines.
Alternatively, you can show the other three formulas starting with the sum formula for sines that we’ve already proved. If you replace β by −β, you’ll get the difference formula. If you replace certain angles by their complements, then you can derive the sum and difference formulas for cosines.