Lattices
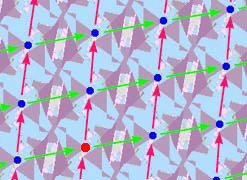 Just by considering the translation symmetries of a pattern we can begin to classify patterns. For any point, the collection of translates of it by translation symmetries of a pattern forms a lattice. In the example at the left, the translates of the one point colored red are indicated by dark blue dots. One translation, call it T, is indicated by the green arrows; it translates right and a bit upward. A different translation, call it U, is indicated by the rose colored arrows; it translates up and a bit right. By taking a composition of these two translations and their inverses, you can construct every other translation symmetry of the pattern. Thus, every translation is of the form TmUn where m and n are integers. Furthermore, you can see what composition you need by seeing where the red dot needs to go. So the lattice of dots corresponds to the translation symmetries.
Just by considering the translation symmetries of a pattern we can begin to classify patterns. For any point, the collection of translates of it by translation symmetries of a pattern forms a lattice. In the example at the left, the translates of the one point colored red are indicated by dark blue dots. One translation, call it T, is indicated by the green arrows; it translates right and a bit upward. A different translation, call it U, is indicated by the rose colored arrows; it translates up and a bit right. By taking a composition of these two translations and their inverses, you can construct every other translation symmetry of the pattern. Thus, every translation is of the form TmUn where m and n are integers. Furthermore, you can see what composition you need by seeing where the red dot needs to go. So the lattice of dots corresponds to the translation symmetries.
Five kinds of lattices
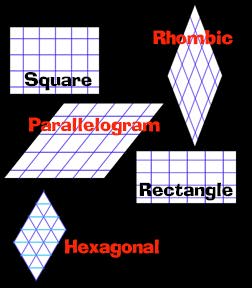 We can classify lattices into five different kinds. If a lattice has a square fundamental region, it's called a square lattice. If it has a 60° rhombus as a fundamental region, it's called a hexagonal lattice. That's because in that case, the points in the lattice nearest any one point in the lattice are the vertices of a regular hexagon. (A rhombus is a parallelogram with equal sides.) If a lattice has a rhombus as a fundamental region, it's a rhombic lattice. (So square and hexagonal lattices are very special rhombic lattices.) If it has a rectangle as a fundamental region, it's a rectangular lattice. And in general, it's a parallelgrammatic lattice.
We can classify lattices into five different kinds. If a lattice has a square fundamental region, it's called a square lattice. If it has a 60° rhombus as a fundamental region, it's called a hexagonal lattice. That's because in that case, the points in the lattice nearest any one point in the lattice are the vertices of a regular hexagon. (A rhombus is a parallelogram with equal sides.) If a lattice has a rhombus as a fundamental region, it's a rhombic lattice. (So square and hexagonal lattices are very special rhombic lattices.) If it has a rectangle as a fundamental region, it's a rectangular lattice. And in general, it's a parallelgrammatic lattice.
If a pattern has a reflection as a symmetry, then its lattice has to be rhombic, rectangular, or square. If it has a 90° rotation, then the lattice must be square. But if it has a 60° rotation or a 120° rotation, the lattice must be hexagonal.
In an upcoming section, there's a description of the 17 wallpaper groups, that is, the symmetry groups of patterns. Lattices are special kinds of patterns, and their symmetry groups of five of these 17 groups.
Lattice
type | Symmetry
group | Rotation
orders | Reflection
Axes |
|---|
| parallelogrammatic | 2 (p2) | 2 | none |
| rectangular | 6 (pmm) | 2 | 90° |
| rhombic | 9 (cmm) | 2 | 90° |
| square | 11 (p4m) | 4 | 45° |
| hexagonal | 17 (p6m) | 6 | 30° |
Parallelogrammatic lattice
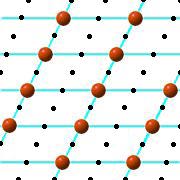 The orange dots indicate the lattice points in the example. The light blue lines outline parallelograms.
Besides the translations of a parallelogrammatic lattice, there are also half-turn symmetries, that is, 180° rotations. Some of the half-turns have lattice points as fixed points, but the fixed points of other half turns occur midway between two lattice points. It may be a little difficult to see these other half-turns, so their fixed points are covered with black dots in this image.
The orange dots indicate the lattice points in the example. The light blue lines outline parallelograms.
Besides the translations of a parallelogrammatic lattice, there are also half-turn symmetries, that is, 180° rotations. Some of the half-turns have lattice points as fixed points, but the fixed points of other half turns occur midway between two lattice points. It may be a little difficult to see these other half-turns, so their fixed points are covered with black dots in this image.
In summary, a parallelogrammatic lattice's symmetry group (number 2, p2) has translations and half-turns, but there are neither reflections nor glide-reflections.
Rectangular lattice
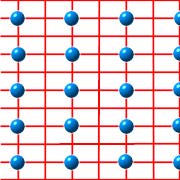 The blue dots indicate the lattice points in the example. Besides the translations and half-turns that every lattice has, rectangular lattices have reflections. The axes of these reflections are drawn in red. Some of the reflection axes pass through the lattice points, but others lie midway between lattice points. The centers of the half-turns lie at the intersections of the reflection axes. There are no glide-reflections (except those which have the same axis as an axis of reflection).
The blue dots indicate the lattice points in the example. Besides the translations and half-turns that every lattice has, rectangular lattices have reflections. The axes of these reflections are drawn in red. Some of the reflection axes pass through the lattice points, but others lie midway between lattice points. The centers of the half-turns lie at the intersections of the reflection axes. There are no glide-reflections (except those which have the same axis as an axis of reflection).
In summary, a rectangular lattice's symmetry group (number 6, pmm) has translations, half-turns, and reflections.
Rhombic lattice
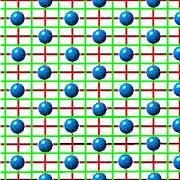 Again, the blue dots indicate the lattice points. Rhombic lattices have translations, half-turns, and reflections, like the rectangular lattices do, but rhombic lattices also have glide reflections. The axes of the glide reflections are shown in green, and appear half-way between the axes of the reflections (shown in red, again). Some of the centers of the the half-turns occur at the intersections of the axes of reflection, but others occur at the intersections of the axes of the glide reflections.
Again, the blue dots indicate the lattice points. Rhombic lattices have translations, half-turns, and reflections, like the rectangular lattices do, but rhombic lattices also have glide reflections. The axes of the glide reflections are shown in green, and appear half-way between the axes of the reflections (shown in red, again). Some of the centers of the the half-turns occur at the intersections of the axes of reflection, but others occur at the intersections of the axes of the glide reflections.
In summary, a rhombic lattice's symmetry group (number 9, cmm) has translations, half-turns, reflections, and glide reflections.
Square lattice
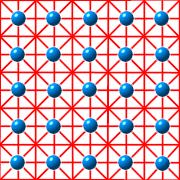 Once more, the blue dots indicate the lattice points. Since a square is simultaneously a rectangle and a rhombus, square lattices have all the symmetries of both rectangular lattices and rhombic lattices. So, square lattices inherit a lot of reflection and glide-reflection axes. The axes of reflection (shown in red in the example) are inclined to each other by 45° so that four axes of reflection pass through each lattice point. The axes of the glide reflections aren't shown, but they are midway between parallel reflection axes. They go in all four directions just as the reflections axes do. They all miss the lattice points.
Once more, the blue dots indicate the lattice points. Since a square is simultaneously a rectangle and a rhombus, square lattices have all the symmetries of both rectangular lattices and rhombic lattices. So, square lattices inherit a lot of reflection and glide-reflection axes. The axes of reflection (shown in red in the example) are inclined to each other by 45° so that four axes of reflection pass through each lattice point. The axes of the glide reflections aren't shown, but they are midway between parallel reflection axes. They go in all four directions just as the reflections axes do. They all miss the lattice points.
Besides numerous half-turns, a square lattice has rotational symmetries of 90° as well. Their centers occur either at the lattice points or equidistant from four neighboring lattice points where four axes of reflection meet.
In summary, a square lattice's symmetry group (number 11, p4m) has translations, rotations of 90° and 180°, reflections, and glide reflections.
Hexagonal lattice
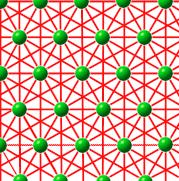 This time green dots indicate the lattice points. What makes this lattice special is that there are 60° rotational symmetries. The fixed points of these rotations are the lattice points. There are many reflections in the symmetry group of the lattice, in fact, six reflection axes meet at each lattice point.
This time green dots indicate the lattice points. What makes this lattice special is that there are 60° rotational symmetries. The fixed points of these rotations are the lattice points. There are many reflections in the symmetry group of the lattice, in fact, six reflection axes meet at each lattice point.
There are glide reflections in this group as well. Their axes (not drawn) are midway between parallel reflection axes
In summary, a hexagonal lattice's symmetry group (number 17, p6m) has translations, rotations of 60°, 120°, and 180°, reflections, and glide reflections.
Up to the table of contents
Back to transformations
On to groups
© 1997.
David E. Joyce
Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610
The address of this file is http://aleph0.clarku.edu/~djoyce/wallpaper/