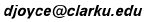The 17 plane symmetry groups
The various planar patterns can by classified by the transformation groups that leave them invariant, their symmetry groups. A mathematical analysis of these groups shows that there are exactly 17 different plane symmetry groups.
Note that clicking on a small image below will take you to a discussion of the associated symmetry group (as will selecting the name of the group in the headings below).
A short table of characteristics of the symmetry groups
There are enough characteristics listed in the table to distinguish the 17 different groups.
Symmetry
group | IUC
notation | Lattice
type | Rotation
orders | Reflection
axes |
|---|
| 1 | p1 | parallelogrammatic | none | none |
| 2 | p2 | parallelogrammatic | 2 | none |
| 3 | pm | rectangle | none | parallel |
| 4 | pg | rectangle | none | none |
| 5 | cm | rhombus | none | parallel |
| 6 | pmm | rectangle | 2 | 90° |
| 7 | pmg | rectangle | 2 | parallel |
| 8 | pgg | rectangle | 2 | none |
| 9 | cmm | rhombus | 2 | 90° |
| 10 | p4 | square | 4 | none |
| 11 | p4m | square | 4 + | 45° |
| 12 | p4g | square | 4 * | 90° |
| 13 | p3 | hexagon | 3 | none |
| 14 | p31m | hexagon | 3 * | 60° |
| 15 | p3m1 | hexagon | 3 + | 30° |
| 16 | p6 | hexagon | 6 | none |
| 17 | p6m | hexagon | 6 | 30° |
| + = all rotation centers lie on reflection axes
* = not all rotation centers on reflection axes |
The IUC notation is the notation for the symmetry group adopted by the
International Union of Crystallography in 1952.
This is the simplest symmetry group. It consists only of translations. There are neither reflections, glide-reflections, nor rotations. The two
translation axes may be inclined at any angle to each other. Its lattice
is parallelogrammatic, so a fundamental region for the symmetry group is the same as that for the translation group, namely, a parallelogram.
This group differs only from the first group in that it contains 180°
rotations, that is, rotations of order 2. As in all symmetry groups there are translations, but there neither reflections nor glide reflections. The two translations axes may be inclined at any angle to each other. The lattice is a parallelogrammatic. A fundamental region for the symmetry group is half of a parallelogram that is a fundamental region for the translation group.
This is the first group that contains reflections. The axes of reflection are parallel to one axis of translation and perpendicular to the other axis of translation. The lattice is rectangular. There are neither rotations nor glide reflections. A fundamental region for the translation group is a rectangle, and one can be chosen that is split by an axis of reflection so that one of the half rectangles forms a fundamental region for the symmetry group.
This is the first group that contains glide reflections. The direction of the glide reflection is parallel to one axis of translation and perpendicular to the other axis of translation. There are neither rotations nor reflections. The lattice is rectanglular, and a rectangular fundamental region for the translation group can be chosen that is split by an axis of a glide reflection so that one of the half rectangles forms a fundamental region for the symmetry group.
This group contains reflections and glide reflections with parallel axes. There are no rotations in this group. The translations may be inclined at any angle to each other, but the axes of the reflections bisect the angle formed by the translations, so the fundamental region for the translation group is a rhombus. A fundamental region for the symmetry group is half the rhombus.
This symmetry group contains perpendicular axes of reflection. There are no glide-reflections or rotations. The lattice is rectanglular, and a rectangle can be chosen for the fundamental region of the translation group so that a quarter-rectangle of it is a fundamental region for the symmetry group.
This group contains both a reflection and a rotation of order 2. The centers of rotations do not lie on the axes of reflection. The lattice is rectangular, and a quarter-rectangle of a fundamental region for the translation group is a fundamental region for the symmetry group.
This group contains no reflections, but it has glide-reflections and half-turns. There are perpendicular axes for the glide reflections, and the centers of the rotations do not lie on these axes. Again, the lattice is rectangular, and a quarter-rectangle of a fundamental region for the translation group is a fundamental region for the symmetry group.
This group has perpendicular reflection axes, as does group 6(pmm), but it also has rotations of order 2. The centers of the rotations do not lie on the reflection axes. The lattice is rhomic, and a quarter of a fundamental region for the translation group is a fundamental region for the symmetry group.
This is the first group with a 90° rotation, that is, a rotation of order 4.
It also has rotations of order 2. The centers of the order-2 rotations are
midway between the centers of the order-4 rotations. There are no
reflections. The lattice is square, and again, a quarter of a fundamental region for the translation group is a fundamental region for the symmetry group.
This group differs from 10 (p4) in that it also has reflections. The axes of reflection are inclined to each other by 45° so that four axes of reflection pass through the centers of the order-4 rotations. In fact, all the rotation centers lie on the reflection axes. The lattice is square, and an eighth, a triangle, of a fundamental region for the translation group is a fundamental region for the symmetry group.
This group also contains reflections and rotations of orders 2 and 4. But the axes of reflection are perpendicular, and none of the rotation centers lie on the reflection axes. Again, the lattice is square, and an eighth of a square fundamental region of the translation group is a fundamental region for the symmetry group.
This is the simplest group that contains a 120°-rotation, that is, a rotation of order 3, and the first one whose lattice is hexagonal.
This group contains reflections (whose axes are inclined at 60° to one another) and rotations of order 3. Some of the centers of rotation lie on the reflection axes, and some do not. The lattice is hexagonal.
This group is similar to the last in that it contains reflections and order-3 rotations. The axes of the reflections are again inclined at 60° to one another, but for this group all of the centers of rotation lie on the reflection axes. Again, the lattice is hexagonal.
This group contains 60° rotations, that is, rotations of order 6. It also
contains rotations of orders 2 and 3, but no reflections. Its lattice is hexagonal.
This most complicated group has rotations of order 2, 3, and 6 as well as
reflections. The axes of reflection meet at all the centers of rotation. At
the centers of the order-6 rotations, six reflection axes meet and are
inclined at 30° to one another. The lattice generator is hexagonal.
Up to the table of contents
Back to groups
On to history
© 1994, 1997.
David E. Joyce
Department of Mathematics and Computer Science
Clark University
Worcester, MA 01610
These files are located at http://www.clarku.edu/~djoyce/wallpaper/