This is an introduction to complex numbers. It includes the mathematics and a little bit of history as well. It is intended for a general audience. The necessary background in a familiarity with ordinary real numbers (all positive and negative numbers and zero) and algebra.
In one section some background in trigonometry is needed as indicated with the  symbol. That section goes further into complex numbers and is optional in an introduction.
symbol. That section goes further into complex numbers and is optional in an introduction.
Table of contents
I. History
II. Mathematics
- 4. The complex plane, addition and subtraction
- Notation, arithmetic operations on C, parallelogram rule, addition as translation, negation and subtraction
- 5. Absolute value
- The unit circle, the triangle inequality
- 6. Multiplication
- Multiplication done algebraically, multiplying a complex number by a real number, multiplication and absolute value, powers of i, roots of unity, multiplying a complex number by i, a geometric interpretation of multiplication
- 7. Angles and polar coordinates
- 8. Reciprocals, conjugation, and division
- Reciprocals done geometrically, complex conjugates, division
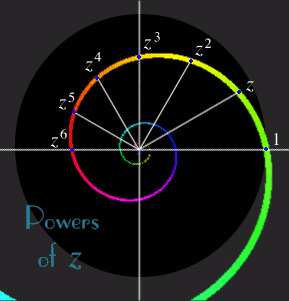
- 9. Powers and roots
- Powers, roots, more roots of unity
 symbol. That section goes further into complex numbers and is optional in an introduction.
symbol. That section goes further into complex numbers and is optional in an introduction.
 symbol. That section goes further into complex numbers and is optional in an introduction.
symbol. That section goes further into complex numbers and is optional in an introduction.