Proposition 41
If a parallelogram has the same base with a triangle and is in the same parallels, then the parallelogram is double the triangle.
Let the parallelogram ABCD have the same base BC with the triangle EBC, and let it be in the same parallels BC and AE.
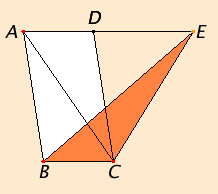
I say that the parallelogram ABCD is double the triangle BEC.
Join AC.
Then the triangle ABC equals the triangle EBC, for it is on the same base BC with it and in the same parallels BC and AE.
But the parallelogram ABCD is double the triangle ABC, for the diameter AC bisects it, so that the parallelogram ABCD is also double the triangle EBC.
Therefore if a parallelogram has the same base with a triangle and is in the same parallels, then the parallelogram is double the triangle.
Q.E.D.