Proposition 43
Let ABCD be a parallelogram, and AC its diameter, and about AC let EH and FG be parallelograms, and BK and KD the so-called complements.
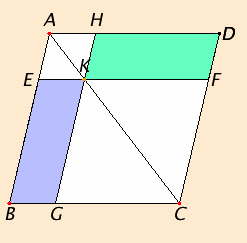
I say that the complement BK equals the complement KD.
Since ABCD is a parallelogram, and AC its diameter, therefore the triangle ABC equals the triangle ACD.
Again, since EH is a parallelogram, and AK is its diameter, therefore the triangle AEK equals the triangle AHK. For the same reason the triangle KFC also equals KGC.
Now, since the triangle AEK equals the triangle AHK, and KFC equals KGC, therefore the triangle AEK together with KGC equals the triangle AHK together with KFC.
And the whole triangle ABC also equals the whole ADC, therefore the remaining complement BK equals the remaining complement KD.
Therefore in any parallelogram the complements of the parallelograms about the diameter equal one another.