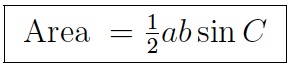
Another is Heron’s formula which gives the area in terms of the three sides of the triangle, specifically, as the square root of the product s(s – a)(s – b)(s – c) where s is the semiperimeter of the triangle, that is, s = (a + b + c)/2.
Here, we’ll consider a formula for the area of a triangle when you know two sides and the included angle of the triangle. Suppose we know the values of the two sides a and b of the triangle, and the included angle C.
As in the proof of the law of sines in the previous section, drop a perpendicular AD from the vertex A of the triangle to the side BC, and label this height h. Then triangle ACD is a right triangle, so sin C equals h/b. Therefore, h = b sin C. Since the area of the triangle is half the base a times the height h, therefore the area also equals half of ab sin C. Although the figure is an acute triangle, you can see from the discussion in the previous section that h = b sin C holds when the triangle is right or obtuse as well. Therefore, we get the general formula
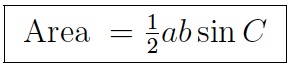
That is to say, the area of a triangle is half the product of two sides times the sine of the included angle.